Abstract
Feedback delay networks (FDNs) belong to a general class of recursive filters which are widely used in sound synthesis and physical modeling applications. We present a numerical technique to compute the modal decomposition of the FDN transfer function. The proposed pole finding algorithm is based on the Ehrlich-Aberth iteration for matrix polynomials and has improved computational performance of up to three orders of magnitude compared to a scalar polynomial root finder. The computational performance is further improved by bounds on the pole location and an approximate iteration step. We demonstrate how explicit knowledge of the FDN’s modal behavior facilitates analysis and improvements for artificial reverberation. The statistical distribution of mode frequency and residue magnitudes demonstrate that relatively few modes contribute a large portion of impulse response energy.

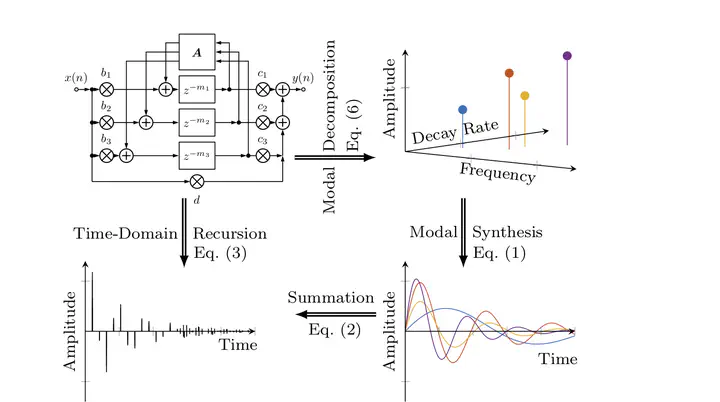
Figure 1: Conceptual overview of modal decomposition and synthesis of a feedback delay network (FDN). $\textit{Top left}$: FDN block diagram with three delay lines $\mathbf{D}_{\mathbf{m}}(z)$, connected via a feedback matrix $\mathbf{A}$, and input and output gains $\mathbf{b}$ and $\mathbf{c}$ for input and output signals $x$ and $y$, respectively. Thick lines indicate multiple signals. $\textit{Top right}$: FDN modes with four parameters each: frequency, decay rate, initial amplitude and phase (not depicted). $\textit{Bottom right}$: Discrete time-domain impulse responses of the resonators corresponding to the FDN modes. $\textit{Bottom left}$: Discrete time-domain impulse response of the FDN.
Statistical Distribution of Residues

Figure 2: Histograms of the residue magnitude with delays $\mathbf{m} = [492,794,1849,1855,1155,1090,78,1957]$ for four different orthogonal matrices $\mathbf{A}_1$, $\mathbf{A}_2$, $\mathbf{A}_3$ and $\mathbf{A}_4$. The four matrices are chosen manually from 1000 random orthogonal matrices to display a variety of residues magnitude distributions.
Impulse responses of FDNs with four different orthogonal matrices $\mathbf{A}_1$, $\mathbf{A}_2$, $\mathbf{A}_3$ and $\mathbf{A}_4$.
Credits
Trackswitch.js was developed by Nils Werner, Stefan Balke, Fabian-Rober Stöter, Meinard Müller and Bernd Edler.