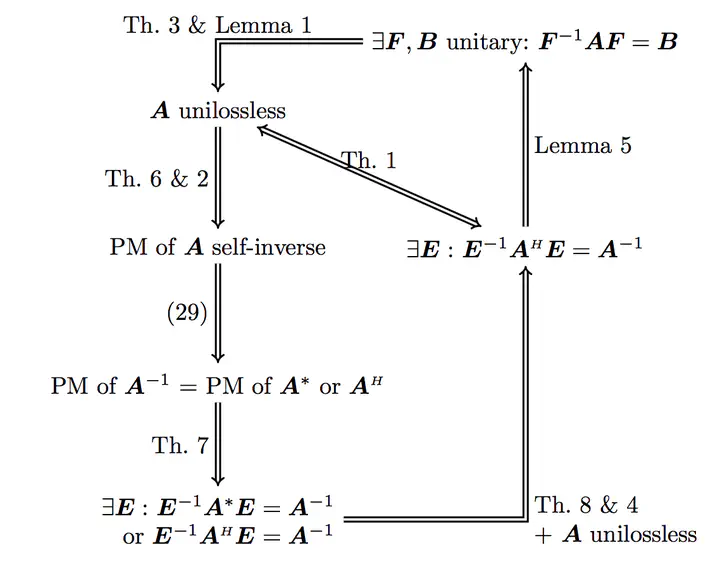
Abstract
Lossless Feedback Delay Networks (FDNs) are commonly used as a design prototype for artificial reverberation algorithms. The lossless property is dependent on the feedback matrix, which connects the output of a set of delays to their inputs, and the lengths of the delays. Both, unitary and triangular feedback matrices are known to constitute lossless FDNs, however, the most general class of lossless feedback matrices has not been identified. In this contribution, it is shown that the FDN is lossless for any set of delays, if all irreducible components of the feedback matrix are diagonally similar to a unitary matrix. The necessity of the generalized class of feedback matrices is demonstrated by examples of FDN designs proposed in literature.