Feedback Structures for a Transfer Function Model of a Circular Vibrating Membrane
Abstract
The attachment of feedback loops to physical or musical systems enables a large variety of possibilities for the modification of the system behavior. Feedback loops may enrich the echo density of feedback delay networks (FDN), or enable the realization of complex boundary conditions in physical simulation models for sound synthesis. Inspired by control theory, a general feedback loop is attached to a model of a vibrating membrane. The membrane model is based on the modal expansion of an initial-boundary value problem formulated in a state-space description. The possibilities of the attached feedback loop are shown by three examples, namely by the introduction of additional mode wise damping; modulation and damping inspired by FDN feedback loops; time-varying modification of the system behavior.
Block Diagram

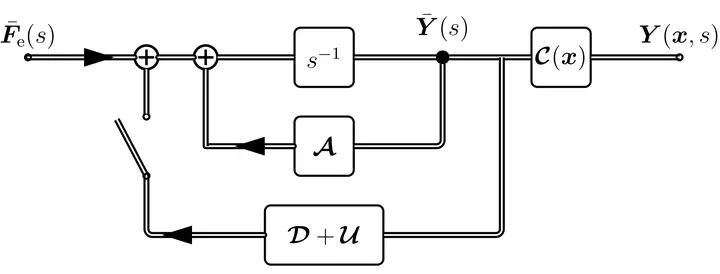
Figure 1: State-space description of the 2D circular membrane in the frequency domain (switch open $\widehat{=}$ open loop system) and the attached feedback loop (switch closed $\widehat{=}$ closed loop system).
Audio Examples
We present various examples of feedback configurations for the proposed system of the circular membrane for sound synthesis.
Damping Only
In the following, we apply time-invariant damping only in the feedback via the diagonal matrix $\mathcal{D} = \textrm{diag}( \dots, d_{\mu}, \dots ) $ and $\mathcal{U} = 0$.
| Damping Type | Damping Coefficients |
|---|---|
| No Damping | $d_{\mu} = 0$ |
| Equal Damping | $d_{\mu}= -2$ |
| Frequency-dependent Damping | $d_{\mu} = -0.001 \cdot k_{n,m}^2/R_0^2$ |
| Tension-like Modulation | $d_{\mu} = 0.05j \cdot k_{n,m}^2/R_0^2$ |
Sound example with various damping feedback loop.
Time Variation
In the following, we apply time-variant coupling only in the feedback via the matrix $\gamma_\textrm{U}[k] \cdot \mathcal{U}$ with $\gamma_\textrm{U}[k] = \alpha \sin( \beta , k 2\pi T)$, where $\alpha$ denotes the time-variation amplitude and $\beta$ denotes the time-variation frequency in Hertz ($\mathcal{D} = 0$).
| Feedback Matrix Type | Time variation Amplitude $\alpha$ | Time variation Frequency $\beta$ |
|---|---|---|
| Identity | 0.00 | 0 |
| Hadamard | 0.01 | 5 |
| Hadamard | 0.05 | 5 |
| Hadamard | 0.02 | 15 |
| Random Orthogonal | 0.02 | 15 |
Sound example with various strength of time-variation.
Experimental Configurations
In the following, we apply time-variant coupling only ($\mathcal{D} = 0$) in the feedback via the matrix with similar parameters as above, but more experimental settings.
| Feedback Matrix Type | Time variation Amplitude $\alpha$ | Time variation Frequency $\beta$ |
|---|---|---|
| Identity | 0.00 | 0 |
| Hadamard | 0.05 | 1.5 |
| Random Orthogonal | 0.11 | 0.1 |
| Random Householder | 0.11 | 1.5 |
| Householder with Ones | 0.11 | 1.5 |
Sound example with more experimental settings.
Credits
Trackswitch.js was developed by Nils Werner, Stefan Balke, Fabian-Rober Stöter, Meinard Müller and Bernd Edler.