Musical Dissonance

The question when musical tones sound in (dis/con)sonance, i.e., in a (un)pleasant accordance, is age-old and reaches back in time to the Ancient Greeks. In modern psychoacoustics, as pioneered by Hermann von Helmholtz, the dissonance is explained through the sensory stimulus of multiple, simultaneously presented simple oscillations, i.e., sinusoids or pure tones. The hypothesis is that musical dissonance can be explained by the sensory roughness of partials, which are close by in frequency. In a perceptual experiment, Plomp and Levelt determined the parameters of such a roughness metric. Later, William Sethares expanded this initial metric into a versatile tool for designing tuning systems with the particular structure of local consonances. Here, we reproduce some of these results in MATLAB.

First, here is the dissonance curve for two sinusoids - one stationary and one raising. The higher the curve, the higher is the predicted sensory dissonance.

Second, multiple of such dissonance curves can be summed to account for extra overtones (red and green). Each time any overtone (red or green) lies within the dissonance curve of another overtone it contributes this amount to the total sensory roughness.

Third, here is the dissonance curve for two tones with seven overtones - one stationary and one raising. The higher the curve, the higher is the predicted sensory dissonance. Some of the dips indicate well-known consonances, e.g., ~500 is the fourth, ~700 is the fifth, 1200 is the octave.

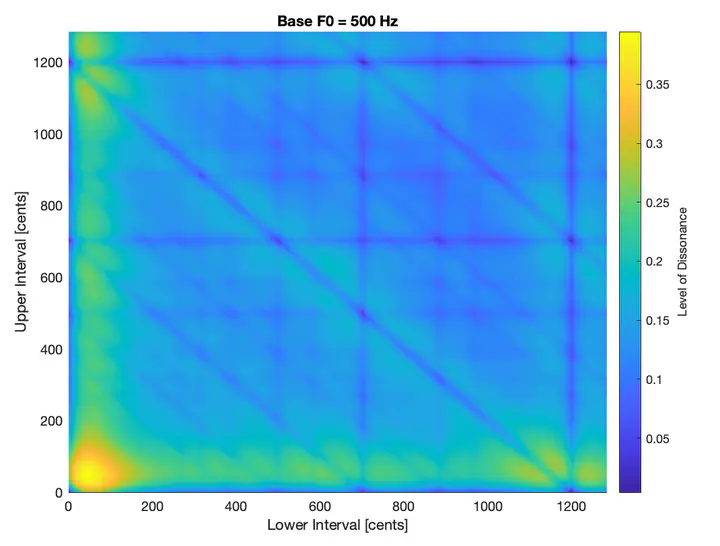
Fourth, the same principle can be now applied to three tones with seven overtones each - one is stationary, and the other two form a lower and a higher interval. The more yellow the curve, the more dissonant is the triad accord. Some of the blue dips are in good accordance with consonant chords, such as the major triad at (400,300).

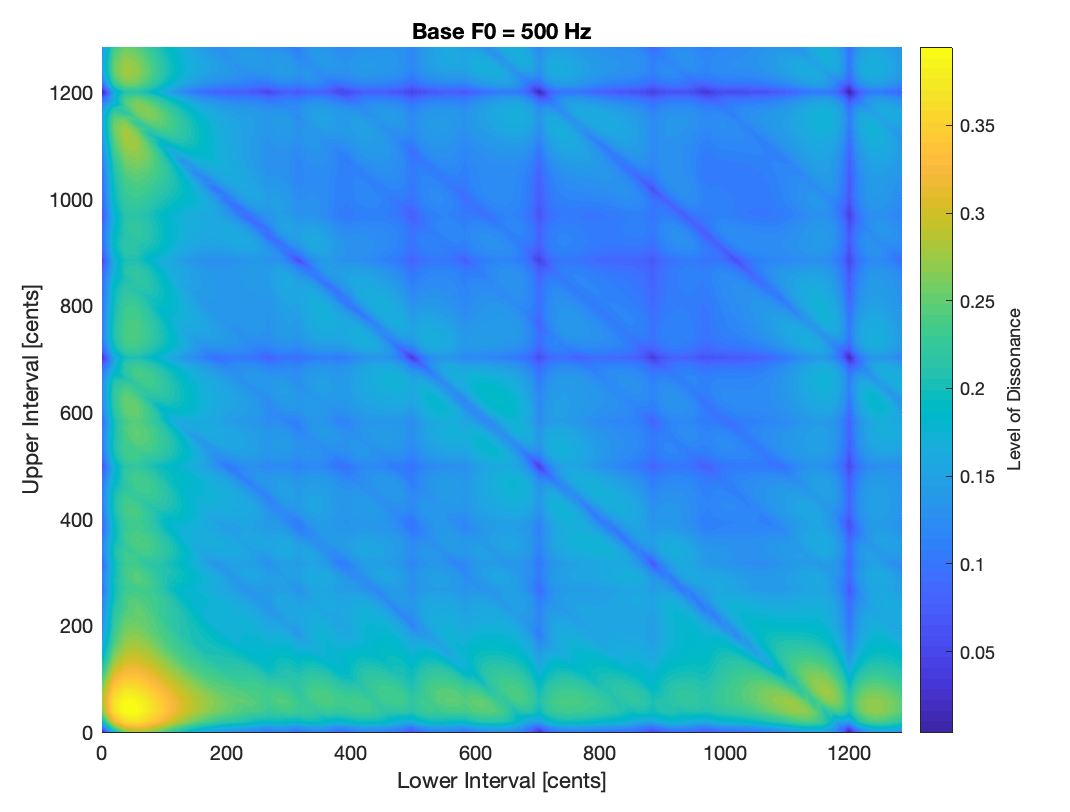
An animated version can also be found in the references code repository. Here, a small demo: