Introduction

In 2018, Välimäki et. al. proposed new signal processing methods to extend a stationary part of an audio signal endlessly¹. It does so by two elegant and efficient techniques: the first method uses convolution with white or velvet noise, while the second method employs the inverse fast Fourier transform (IFFT) with randomized phase. Several impressive sound examples are provided on the companion page including this illustrative video of click-free looping of the extended sounds.

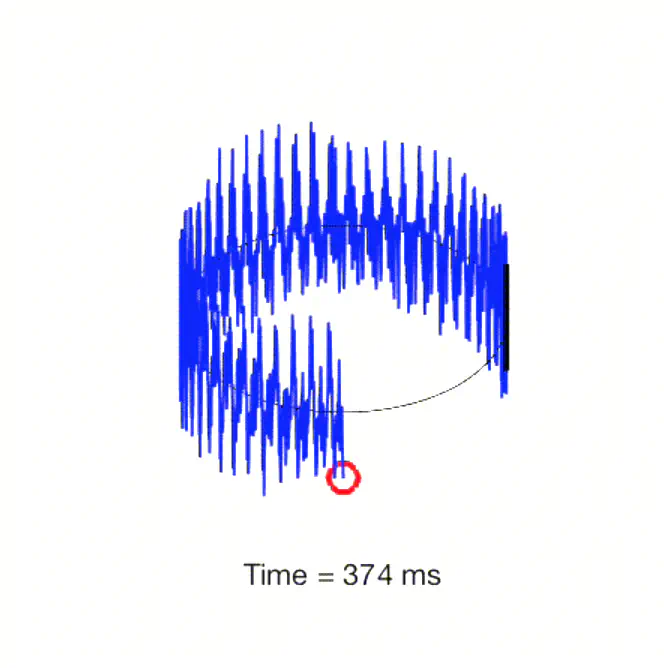
**Figure 1:** Click-free looping of extended sounds created with the IFFT method. Notice that the time axis is circular. This video is reproduced with the courtesy of the original authors.

Curiously (and as noted in this paper), the IFFT creates naturally sounds which loop click-free. The article mentions the circular convolution property of the discrete Fourier transform (DFT) but does not give further detail on this matter. In this post, I will attempt to shed some more light on this matter. The Matlab code for all presented examples can be found here.

Proposed Method

For illustration, I will use a most simple sound sample - a piece of a sine wave - which should be stretched by the proposed method. It should be mentioned that the proposed methods were deliberately developed for non-tonal sounds such that a single sine wave is somewhat out-of-scope. I will use this example, nonetheless, as it clearly shows the underlying signal processing idea. The sample is 50 ms long and has a frequency of 412.7 Hz at 48k sampling frequency. The choice of this odd frequency will come apparent in the next step.

**Figure 2:** Original sample.

Circular Convolution

Because the DFT discretizes the frequency domain, we know that the time-domain is interpreted as periodically repeating. Thus, by transforming the sine wave sample into the frequency domain via the DFT, we implicitly change the sample into this:

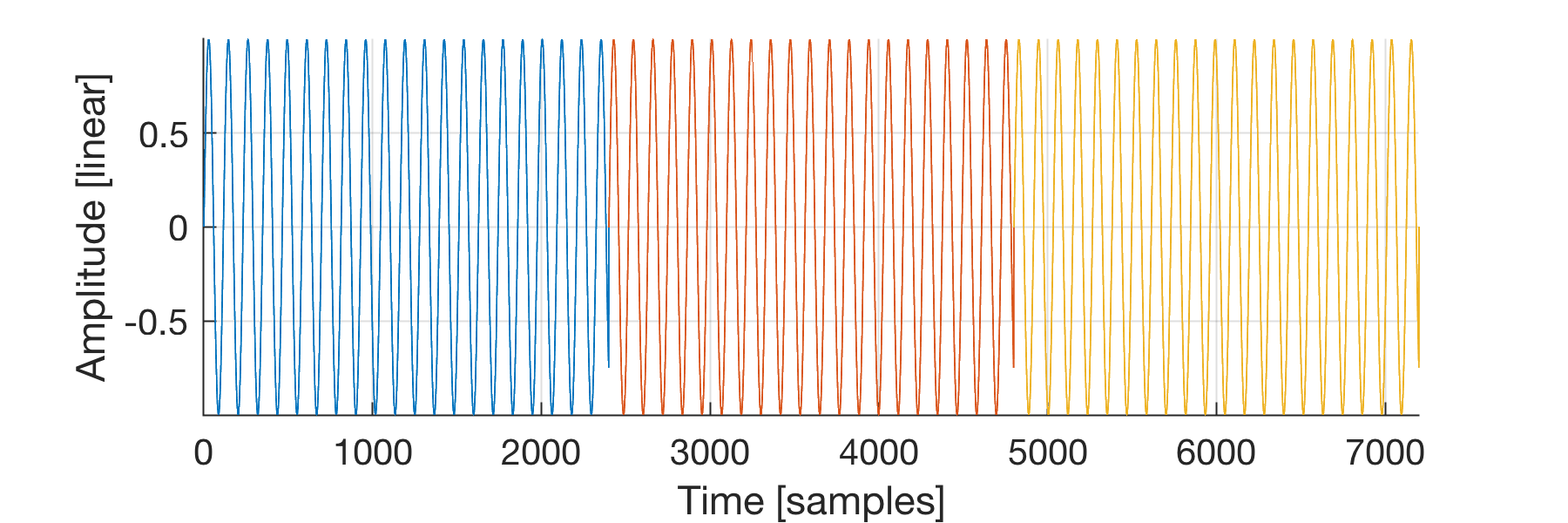**Figure 3:** Repeated original sample.

Other than in exceptional cases, there will be a click at the boundaries of the original sample, which is well-audible and can be distracting for musical sampling.

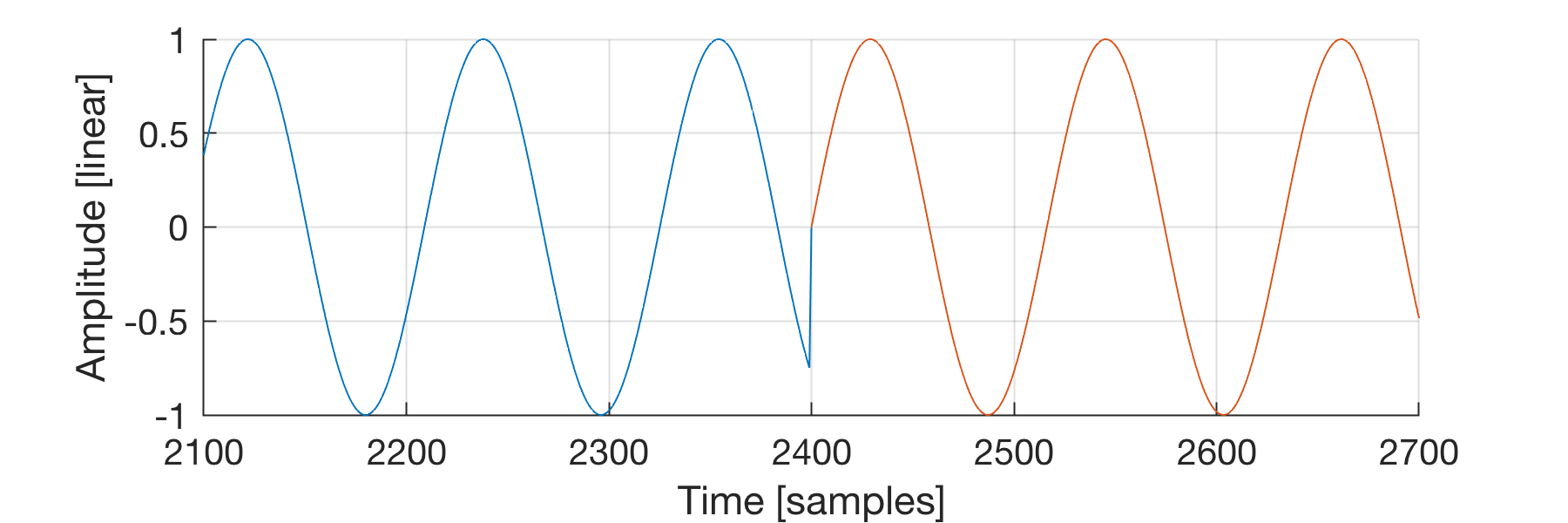**Figure 4:** Zoom on the repetition boundary of the original sample in Fig. 3.

Repeated Original Sample

Randomization

The proposed method now replaces the original phase with random numbers while maintaining the magnitude of the frequency response.

**Figure 5:** Magnitude response of the original and altered sample. **Figure 6:** Orginal and randomized phase response.

Click-free Looping

Now, we apply the IFFT to the altered frequency response. The resulting time-domain signal is given in the next plot:

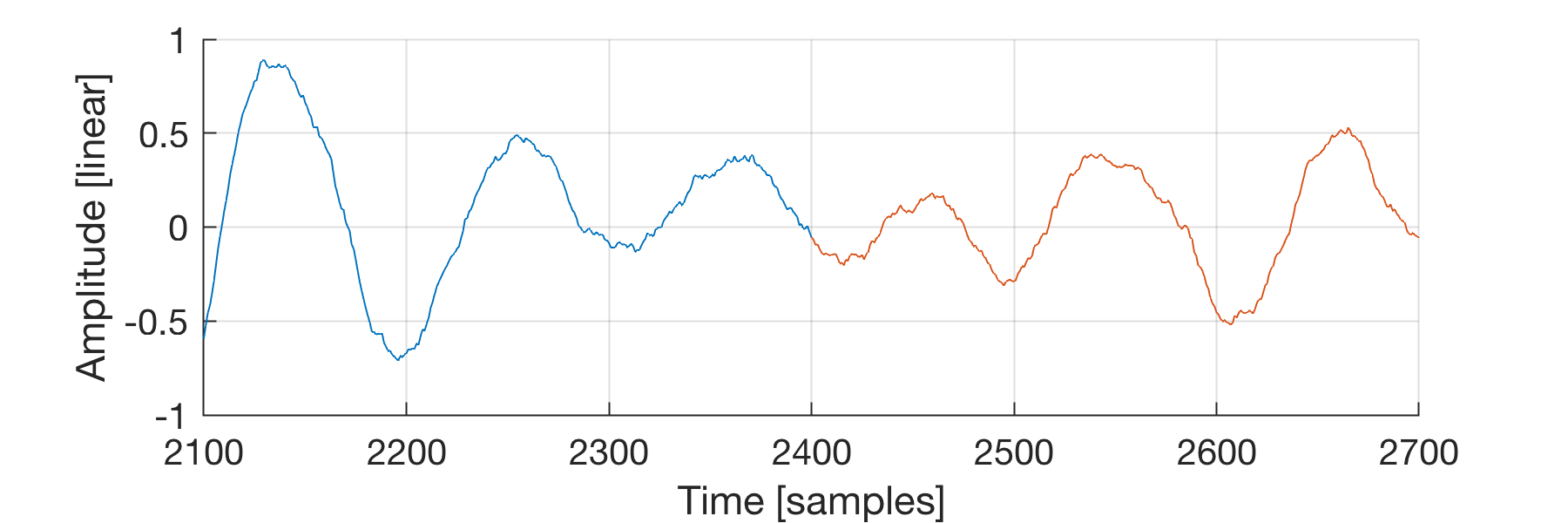**Figure 7:** Zoom on the repetition boundary of the altered sample.

And when zooming in on the boundary, we see that the repetition goes smoothly, and the repetition sounds click-free:

Repeated Randomized Sample
Repeated Stretched Sample

The second sound example follows the same procedure described above except that it adds zero-padding to the original sample before applying the DFT. In this case, I have added enough zeros such that the stretched sample from the IFFT is 3 seconds long.

However instead of the click, now, a constant noise is audible. And that’s precisely where the energy of the repetition click went. A sudden change in the signal is a broadband click. Due to the randomized phase, this broadband click energy is no longer concentrated in time but spread over the full length of the sample.

Windowing

While this added noise is no problem for the extension of noisy samples (the original intention), clean tonal signals might be impaired. A straightforward improvement can be achieved if the repetition click is reduced in the first place by windowing.

**Figure 8:** Windowed original sample with Hann window.

Repeated Windowed Sample

While the windowing introduces amplitude modulation in the original sample, once processed with zero-padding the proposed IFFT method, we get a cleaner result

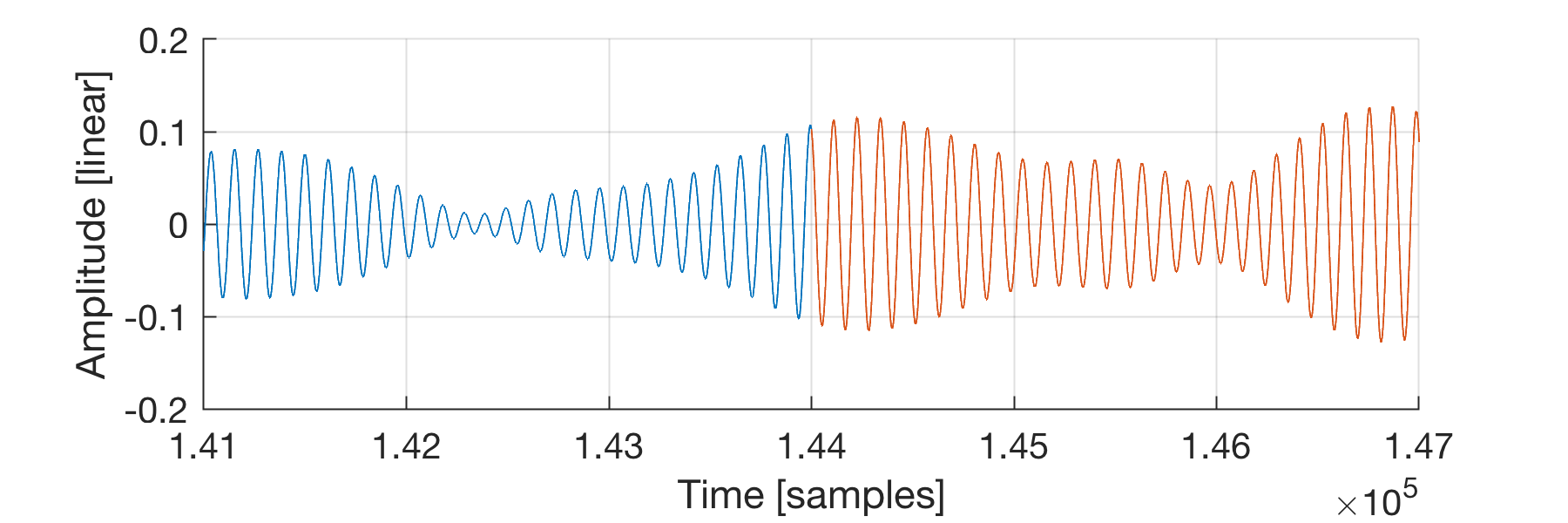**Figure 9:** Zoom on the repetition boundary of the windowed and stretched sample.

Repeated Windowed and Stretched Sample

Conclusion

Hopefully, these few ideas expand on the beautifully elegant method proposed to extend short sound samples into endless sounds. In the future, I like to see more work on this problem to further improve the creation of flexible and excellent sounding sampling machines.

---

1. Välimäki, V., Rämö, J., & Esqueda, F. (2018). Creating endless sounds (pp. 32–39). Presented at the Proc. Int. Conf. Digital Audio Effects (DAFx), Aveiro, Portugal. ↩︎