Distance rendering and perception of nearby virtual sound sources with a near-field filter model
by S. Spagnol, E. Tavazzi, and F. Avanzini in Applied Acoustics, vol. 115, pp. 61-73, Jan. 2017.
Reproduce in Code (c) Sebastian Jiro Schlecht: 20. November 2018
Contents
Introduction
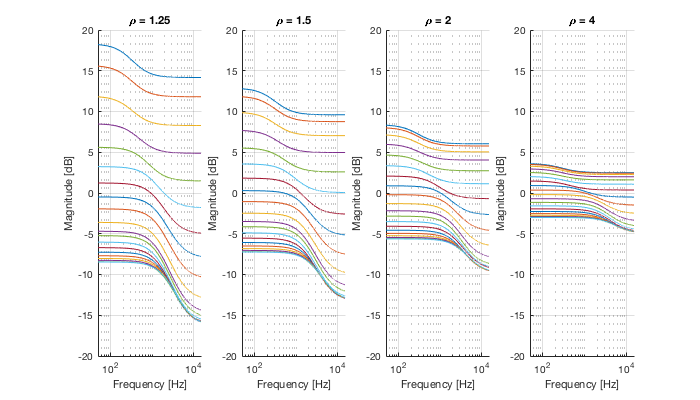
In this tutorial, we reproduce Fig. 1. However in contrast to the publication, we use the filter approximation suggest in the paper.
Initialization
clear; clc; close all;
fftSize = 2^12;
plotIt = 1;
Create plots
for rho = [1.25, 1.5, 2.0, 4.0] H = []; for alpha = linspace(0,pi,20) % Compute filter [num,den,fs] = nearFieldModel(alpha, rho); [H(:,end+1),w] = freqz(num, den, fftSize, fs); end % plot figure(1); subplot(1,4,plotIt); hold on; grid on; plot(w,mag2db(abs(H))) set(gca,'XScale','log'); title(['\rho = ' num2str(rho)]) xlabel('Frequency [Hz]'); ylabel('Magnitude [dB]'); xlim([50 15000]); ylim([-20 20]); plotIt = plotIt + 1; end set(gcf,'pos',[10 10 700 400])