Contents
- La Budde's Method For Computing Characteristic Polynomials
- Introduction
- Speed comparison
- Plot performance results
Called Functions
La Budde's Method For Computing Characteristic Polynomials
by Rizwana Rehman and Ilse C.F. Ipsen in arXiv, April 2011
Reproduce in Code (c) Sebastian Jiro Schlecht: Monday, 10. December 2018
clear; clc; close all;
Introduction
In this example, we reproduce a fast algorithm (Algorithm 2) to computer the characteristic polynomial of a square matrix and compare the output to the MATLAB build-in function charPoly.
N = 12; A = randn(N) + 1i*randn(N); A = A / N; disp('Comparison of Matlab charpoly and LaBudde charpoly') %%----------------- disp('Matlab') tic pMatlab = charpoly(A); toc disp(pMatlab) %%----------------- disp('LaBudde') tic pFast = fastCharPoly( A ); toc disp(pFast) %%compare disp('Compare error') disp(pMatlab - pFast)
Comparison of Matlab charpoly and LaBudde charpoly Matlab Elapsed time is 0.729862 seconds. Columns 1 through 4 1.0000 + 0.0000i -0.3884 - 0.2123i 0.1163 + 0.0161i -0.0139 + 0.0002i Columns 5 through 8 0.0009 - 0.0046i 0.0027 + 0.0009i -0.0004 - 0.0003i 0.0001 + 0.0003i Columns 9 through 12 -0.0000 + 0.0001i -0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i Column 13 -0.0000 + 0.0000i LaBudde Elapsed time is 0.000753 seconds. Columns 1 through 4 1.0000 + 0.0000i -0.3884 - 0.2123i 0.1163 + 0.0161i -0.0139 + 0.0002i Columns 5 through 8 0.0009 - 0.0046i 0.0027 + 0.0009i -0.0004 - 0.0003i 0.0001 + 0.0003i Columns 9 through 12 -0.0000 + 0.0001i -0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i Column 13 -0.0000 + 0.0000i Compare error 1.0e-15 * Columns 1 through 4 0.0000 + 0.0000i 0.0555 - 0.1110i 0.0278 + 0.1249i -0.0069 - 0.0304i Columns 5 through 8 0.0159 - 0.0052i 0.0009 + 0.0011i 0.0005 - 0.0001i 0.0002 + 0.0001i Columns 9 through 12 0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i Column 13 -0.0000 + 0.0000i
Speed comparison
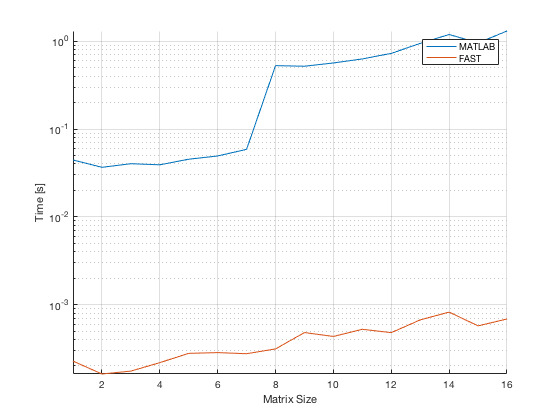
We compare the performance of fastCharPoly to the MATLAB build-in function charPoly. It can be seen that fastCharPoly is more than 100 times faster.
matrixSizes = 1:16; numberOfRepetitions = 5; performanceTime_MATLAB = zeros(length(matrixSizes),numberOfRepetitions); performanceTime_FAST = zeros(length(matrixSizes),numberOfRepetitions); for N = matrixSizes % disp(matrixSize) for repetition = 1:numberOfRepetitions A = randn(N) + 1i*randn(N); A = A / N; tic pMatlab = charpoly( A ); performanceTime_MATLAB(N,repetition) = toc; tic pFast = fastCharPoly( A ); performanceTime_FAST(N,repetition) = toc; if max(abs(pMatlab - pFast)./pMatlab) < 1e-7 % disp('OK') else warning(['Results deviate by ' num2str(max(abs(pMatlab - pFast)))]) end end end
Plot performance results
averagePerformanceTime_MATLAB = mean(performanceTime_MATLAB,2); averagePerformanceTime_FAST = mean(performanceTime_FAST,2); figure(1); hold on; grid on; plot(matrixSizes,averagePerformanceTime_MATLAB) plot(matrixSizes,averagePerformanceTime_FAST) legend({'MATLAB','FAST'}) xlabel('Matrix Size') ylabel('Time [s]') set(gca,'YScale','log'); axis tight;